Interactive Polar Calculus with SageMath: Area, Arc Length, Multivariable Limits, and Continuity Explained (Part 2)

Part 2: Real-Life Applications of Polar Coordinates

Polar coordinates aren't just mathematical curiosities—they're deeply embedded in real-world phenomena across astronomy, engineering, nature, and design. Let’s explore some fascinating, realistic applications!

🚀 Modeling Orbital Paths in Space Exploration

In astronomy, polar coordinates are indispensable for describing the elliptical orbits of planets, moons, and satellites. The fundamental equation:

r(θ) = l / [1 + e cos(θ)]

Where:

• l : Semi-latus rectum
• e : Eccentricity of the orbit

This model predicts the distance r(θ) of a celestial object from its focus (e.g., the sun).

🌸 Nature’s Designs: Petal Shapes, Hurricanes, and Shells

Nature’s patterns often reflect polar coordinate magic:

• Flowers: Rose curves like r = acos(kθ) model petal arrangements.
• Hurricanes: The spiral arms of hurricanes resemble exponential spirals in polar form.
• Seashells: Nautilus shells grow in spirals modeled by polar equations.

🌀 Meteorologists, botanists, and biomimetic engineers study these curves to predict storms, understand growth, and design new materials.

⚙️ Limaçons and Mechanical Engineering Marvels

The limaçon curve:

r= a + bcos(θ)

Features bulges and loops crucial in:

• Cam Profiles: Ensuring smooth engine valve operation.
• Gear Design: Optimizing gear tooth profiles to reduce wear.
• Robotics: Planning precise robotic arm movements based on polar motions.

⚙️ Polar curves ensure machines run efficiently, robots move precisely, and mechanical components last longer.

🎨 Art, Architecture, and Urban Design

Polar coordinates influence artistic and structural designs:

• Stained Glass Windows: Iconic rose windows, like at Notre-Dame, are based on rose curves.
• Tiled Floors and Roundabouts: Symmetrical floor mosaics and urban roundabout layouts often reflect polar symmetry.
• Modern Art Installations: Interactive sculptures use polar spirals to guide viewer movement.

🎨 Polar graphs combine mathematical beauty and practical elegance in architecture and public spaces.

🛡️ Defense and Surveillance Systems

In radar and sonar technology, polar coordinates model how signals radiate outward and reflect back:

• Air Traffic Control: Tracking planes' real-time positions.
• Marine Navigation: Locating ships and submarines.
• Missile Guidance: Accurate target tracking and interception.

🎯 Polar mathematics underpins critical safety, defense, and navigation systems worldwide.

📈 Visualizing Polar Curves with SageMath

Here’s how you can visualize polar curves using SageMath:

Rose Curve Example

Plotting a 3-petaled rose:

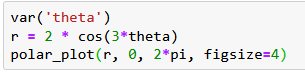
This shows a symmetric flower shape with k=3 petals!

Limaçon Curve Example

Visualizing a limaçon with an inner loop:

Changing 𝑎 and b alters the curve's shape, creating loops or bulges.

Hurricane Spiral Simulation

Approximate a hurricane spiral using an exponential spiral:

This simulates spiral growth, like in storms and galaxies!

🔥 Conclusion: Polar Coordinates Mirror the World

From spacecraft trajectories to hurricane spirals, from flower petals to gear mechanics, polar coordinates unlock the hidden order behind nature, technology, and art.

By experimenting with tools like SageMath, we can not only visualize but also deepen our understanding of the stunning connections between math and reality.

✨ Dive into the world of polar curves—and see the universe unfold before your eyes!

🌟 Quick Fact Highlights

Field	Polar Coordinate Application
Space Exploration	Modeling satellite and spacecraft orbits 🚀
Climate Science	Predicting hurricane spiral arms 🌀
Mechanical Engineering	Designing cams and gears ⚙️
Robotics	Planning robotic arm motion 🤖
Art & Architecture	Crafting rose windows and floor mosaics 🎨
Defense Systems	Tracking objects with radar 🎯

✨ What's Next?

Stay tuned! Get ready to bring polar curves to life through calculus — and master the art of precise measurement, motion, and structure in the polar world!

Part 3: Core Calculus Problems with Polar Curves

Now that we've explored real-world applications, it's time to dive deeper into calculus with polar coordinates!

➡️ Tangents to Polar Curves

How to find and plot tangent lines at specific points.

Example: Explore tangents for the curve:

r = 1 + 2cos(2θ)

➡️ Area Calculations

How to calculate the area enclosed by a single polar curve or between two curves.

Example: Find the area enclosed by a classic limaçon.

➡️ Arc Length

How to measure the length of beautiful polar curves.

Example: Compute the arc length of a spiral segment.